Sometimes the amazed reaction of a student becomes the high point of a day or week.
Discussing series in Calculus class, and one student brings up the example of how
They've obviously heard this one before, but one student up front mutters, "They say that, but I don't see how it's possible." I think I first saw this proof back in 8th grade, from my then teacher Eugene Thompson. I think the idea of converting repeating decimals to fractions was part of the curriculum, and I never checked if that's still something in the middle school standards.
But I offered, "I can prove it pretty quickly to you, if you like." Over half the class nodded and vocalized assent. Perhaps nobody has every bothered to show them this. So I began (most of my math friends know these steps, so bear with me).
I checked, and everyone was okay with this step. So I continued.
Again, I checked. Everybody was okay this this step. So I said I would subtract the first from the second
A third time, I paused and confirm everybody was okay with my steps. No funny business.
This is the result of the subtraction. Still very straightforward. Of course, next I divide both sides by 9.
"Whoa! Wait a second! How did that happen?" A student in back who wasn't paying attention asked me to do it again. Another student asked if it always works (by which I think she meant does that work for all repeating decimals). So I showed them again with 0.6666 repeating. I had them amazed and enthralled.
It was a ten minute diversion in a 98 minute class. I think it was worth it.



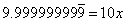
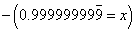

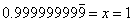
No comments:
Post a Comment