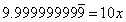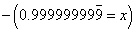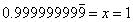Lissajous

Finally, I've got some moderate success to report with my Lissajous figure.

Yesterday I tried printing with raft and supports (because of printing difficulties without).

somehow reminds me of the World Series trophy

So the figure printed, although it took a long time (a little over two hours) because extruding all the extra plastic for the supports was a significant addition. Then, afterwards, the supports needed to be broken out.

removing supports with my handy dandy leatherman tool

And that's where the issues arose. Even though I repaired the .stl file with visCAM and netfabb, the intersections points were still weak, and I could see light coming through them. They didn't appear to be solid connections. The physical stress of breaking off the supports was more than the structure could deal with, and it began to break. "Don't worry," people told me, "you can superglue it back together." But that's not the point. I wanted to print as a single piece.

printed with supports, mostly removed, but lost integrity of the plot in the process

I thought of taking the piece home and use my Dremel rotary tool to get the rest of the supports off. But I left school in a hurry, and neglected to pack it.

While doing whatever it is I do when not at work, an idea came to me -- rotate the figure 90 degrees in the y-z plane. The problem had been my horizontal spans had been too long, but by rotating I'd change those horizontals to verticals. Verticals don't typically have as much issue printing.

So that's what I tried this morning. Using the exact same .stl file, I used MakerWare to rotate, and printed with rafts but without supports. Success!

small raft under each loop

printing complete. I like the wisp of PLA trailing back to the print head.

before removing the rafts

after removing the rafts. hand modeling courtesy of Eloise.

If anyone wants, here's the .thing on thingiverse.

*** change history ***
4/19/2014 added link to .thing file
4/16/2014 corrected spelling

Fixing 3D Designs

One of the things George warned us about is the possiblity that Mathematica might create an invalid .stl file when it exports. I don't understand the bug exactly, but somehow when it draws the .stl, which is composed of many triangles which have orientation, it might create some triangles either with orientation reversed, or with edges that don't align correctly. He suggested two tools to detect and fix these errors.

Since I had a problem printing my lissajous figure (see image below), I thought it might be from this sort of error. I downloaded and installed the first tool, VisCam, and it indeed found 24 flipped triangles. But this tool cannot fix. It can only check for errors. So I downloaded and installed the second tool, NetFabb. It took a while for me to figure this one out, but eventually I found the menu to check, and the menu to repair errors. But it wants to save only in its own format, and it took me a while to discover how to export back to .stl. Turns out the part has to be selected for this option to appear. Okay, obvious, but it took me a while.

Next week I'll try printing the repaired part, and I'll report back on how it goes.

Infinite Series

Sometimes the amazed reaction of a student becomes the high point of a day or week.

Discussing series in Calculus class, and one student brings up the example of how

They've obviously heard this one before, but one student up front mutters, "They say that, but I don't see how it's possible." I think I first saw this proof back in 8th grade, from my then teacher Eugene Thompson. I think the idea of converting repeating decimals to fractions was part of the curriculum, and I never checked if that's still something in the middle school standards.

But I offered, "I can prove it pretty quickly to you, if you like." Over half the class nodded and vocalized assent. Perhaps nobody has every bothered to show them this. So I began (most of my math friends know these steps, so bear with me).

I checked, and everyone was okay with this step. So I continued.

Again, I checked. Everybody was okay this this step. So I said I would subtract the first from the second

A third time, I paused and confirm everybody was okay with my steps. No funny business.

This is the result of the subtraction. Still very straightforward. Of course, next I divide both sides by 9.

"Whoa! Wait a second! How did that happen?" A student in back who wasn't paying attention asked me to do it again. Another student asked if it always works (by which I think she meant does that work for all repeating decimals). So I showed them again with 0.6666 repeating. I had them amazed and enthralled.

It was a ten minute diversion in a 98 minute class. I think it was worth it.

Checksums for Groupwork

I was trying to refresh my memory of what Jill Gough has showed me about leveled assessments, and so I was searching her blog Experiments in Learning by Doing. In that process, I came across a link she had to this post from Function of Time, blogged by Kate Nowak. I was intrigued by the idea, and decided to try to adapt it to my classroom.

I teach three sections of Geometry this year, one freshmen and two sophomore. I chose to write an activity for Distance Formula using this self-check routine. With the help of my awesome student teacher, this year I've managed to make meaningful groupwork the norm in my classroom. So the students are used to a lot of the typical classroom rules of groupwork (ask each other before asking teacher, work with your own group rather than others, etc). I wouldn't recommend trying this on the first day of groups.

We've spent a few days applying Pythagorean theorem to triangle problems. The next task in our pacing calendar is to draw the tie to distance formula. I introduced the idea with a brief explanation showing we can calculate distance between points not on the same vertical or horizontal line by making those points endpoints of a segment corresponding to the hypotenuse of a right triangle whose legs are horizontal and vertical. I try to emphasize that the distance formula, littered with subscripts and pesky subtractions and additions and exponents and radicals, is really just the Pythagorean theorem, which my students all knew before they ever met me.

So, we worked a few problems together. Then I let them loose with their worksheets.

As Ms. Nowak describes, I had groupings of four students, four worksheets of graduated difficulty on differently colored paper, the colors posted in order on the board, with the checksum folded inside.

I gave the verbal instructions, as this task is a little different than other group tasks we've done. Each student is to do one problem per sheet. I asked them to write their name next to the problem they worked. When all four problems are finished, add the numerical answers and check it against the checksum on the whiteboard. My classroom calculators were made available to students who don't carry their own.

The orange and blue sheets had straightforward distance problems; orange with integers and blue with radicals. The green sheet gave distances and three of four coordinates, asking for the missing coordinate. The yellow sheet gave vertices of polygons and asked things about the underlying polygons.

Things didn't go so well for the first class. I noticed almost all groups started with the yellow (most difficult) sheet, and didn't make any progress. My suggestion they start with the orange (easier) met few results. When the period bell rang, no group had completed any entire single sheet.

For the second class, I began by only distributing the orange and blue sheets. As groups made progress, I gave them the green, and then the yellow. The second class is my freshmen (ninth grade) who typically have difficulty focusing on work. Even so, they made much better progress than the first group. I used the same distribution pattern for the third class, and they did the most work of all. Almost all the groups at least began work on the last sheet.

I really like the self-reliance aspect of this idea, and will use it again for future lessons. (My paper is Wausau Astrobrights, which I love.)

*** edit 6 April 2014 ***
a link to the worksheets I used