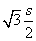At my school, Friday was a sort of "reward" day. Students with some definition of good attendance were taken on a trip to Six Flags amusement park. (The students remaining may have viewed it is a "punishment" day.) I was unsure what numbers I would have left, being as it would be primarily consisting of students who don't attend regularly, on top of which we weren't given a list in advance. So I planned on not continuing the sequence of lessons I had been in, since a large number were likely to be absent. My classes are called Algebra II, and students are primarily 11th and 12th graders, with some 10th graders as well. Students have all passed Algebra I, but in many cases have not yet passed the NY Algebra I Regents exam.
The ideas involved build on some of the ideas discussed by Edith Somervell in her 1906 A Rhythmic Approach to Mathematics. In my 45 minute periods, I narrowed my focus to three short explorations.
I began with a set of Cartesian axes. I provided students with square graph paper and rulers, and instructed them to draw a pair of axes, and the use the ruler in order to make lines as straight as possible. I wanted to axes roughly centered on the paper, but did not instruct so. I knew from experience that most of my students will draw things in the center of a sheet of graph paper, regardless what scale might be appropriate, but I was also counting on some students NOT putting the origin in the center, so we could have a discussion about how that affected our ability to draw the results.
I asked students to name a pair of number that adds to 10, such as 2 and 8. I instructed them to connect 2 on the x-axis to 8 on the y-axis with a straight line. I asked for another pair of numbers, and similarly connect one on the x-axis to the other on the y-axis. I repeated a few times, and the asked students to connect every such pair of numbers they could think of. I waited for students to ask, "How about 0 and 10?" I asked if 0 plus 10 equals 10? Yes. What does it look like when I draw the 0-10 line? Nothing because it's on the axis. So, the full answer is, yes we can use 0-10, but it doesn't add to our figure because it lies on an axis. I similarly waited for students to ask about negative numbers. I asked if there was something we could add to negative 2 that sums to 10. "Yes, positive 12." So we can draw it. In all classes these questions eventually came out. If they had not, I would have asked them, but wanted to wait for students to generate them if possible.
 Errors. Many students in the first class connected to two axis values with big looping curves, despite the instruction to use the ruler to make the line as straight as possible, and despite my modeling this on the board up front. A few students, instead of drawing lines, marked the points whose coordinates add up to ten. I made sure to model more resolutely in subsequent periods, and circulated more busily between groups of desks.
Errors. Many students in the first class connected to two axis values with big looping curves, despite the instruction to use the ruler to make the line as straight as possible, and despite my modeling this on the board up front. A few students, instead of drawing lines, marked the points whose coordinates add up to ten. I made sure to model more resolutely in subsequent periods, and circulated more busily between groups of desks.
Once there were a few students with enough lines drawn to discern a shape, I held one up, and asked the class what they though would form as they continued drawing lines. The actual answer is parabola, but no student came up with this. Some students were convinced it would form a circle. I did not correct them, but instead suggested they continue to think about it as they added lines.
 But I did not allow much more time on the Cartesian graph. My main point was to work with circles of numbered points. I distributed copies of 30-dot circles, as shown. Asked what they noticed about the circles. I want to elicit how many dots there are, what the smallest number is, and what the largest number is. Before proceeding, I wanted to make sure they realize that this is one of the cases where we start counting at zero.
But I did not allow much more time on the Cartesian graph. My main point was to work with circles of numbered points. I distributed copies of 30-dot circles, as shown. Asked what they noticed about the circles. I want to elicit how many dots there are, what the smallest number is, and what the largest number is. Before proceeding, I wanted to make sure they realize that this is one of the cases where we start counting at zero.
I began by discussing "clock arithmetic." I tried using the more mathematical term, modular arithmetic, but each class clearly preferred "clock," so I went back to that. We tried examples until I was confident they knew how to continue around the circle once they reached the highest number.
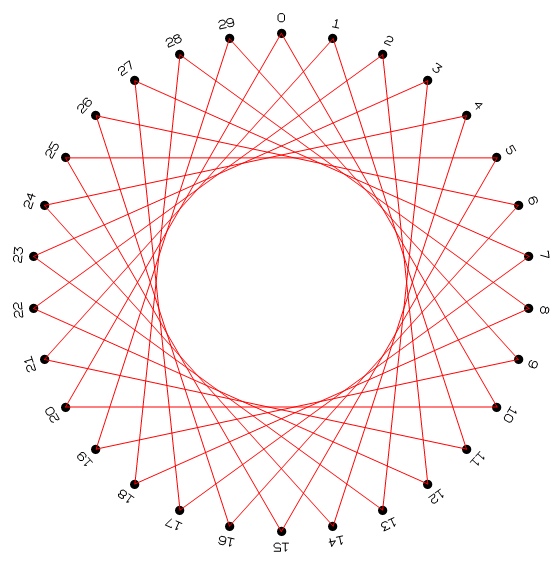 I asked students to choose a number between 1 and 30. (One student chose 15, to interesting result.) Then I instructed they connect each dot, via straight line, to the dot that was their number higher. If they chose 10, they would connect 0 to 10, 1 to 11, 2 to 12, and so on. I reconfirmed they understood modulo. Where would 19 connect? 29. How about 20? 30. But we don't have a 30, so where do we go instead. Oh.
I asked students to choose a number between 1 and 30. (One student chose 15, to interesting result.) Then I instructed they connect each dot, via straight line, to the dot that was their number higher. If they chose 10, they would connect 0 to 10, 1 to 11, 2 to 12, and so on. I reconfirmed they understood modulo. Where would 19 connect? 29. How about 20? 30. But we don't have a 30, so where do we go instead. Oh.
I instructed them to continue until all numbered dots have been connected. The figure shows what it would look like if their chosen number were 10. Again, I asked how they would describe the shape they had made. But I had a few students with different numbers hold up their drawings. How are they different. A conjecture formed that "the larger the number, the smaller the circle. In some classes students had chose numbers larger than 15, so I was able to challenge the conjecture, and students struggled to explain that behavior. In the class with a student who chose 15 as her number, all lines intersected at a point in the center, and I asked students if that fit with their conjecture.
Errors. Some students had difficulty understanding the mapping idea, and kept connecting the same dot over and over again to different places on the circle. In the first period, I wrote the numbers as ordered pairs, which may have added to that confusion. From then on, I wrote the pairs with an arrow between (e.g. 1-->11, 4-->14), to emphasize the mapping. I had fewer errors with this notation, but still had to correct a few students.
Some students didn't understand that each of the 30 dots had to be the origin of a connecting line, and each had to be the terminal of a connecting line. At the end there should be two lines for each point. These students stopped early, saying they were done. I showed them how to continue, covering all their dots.
Depending on timing, I went two directions from here. If there was time, and for students who finished quickly, I suggested they choose another number, and with a different color pen they repeat the process.
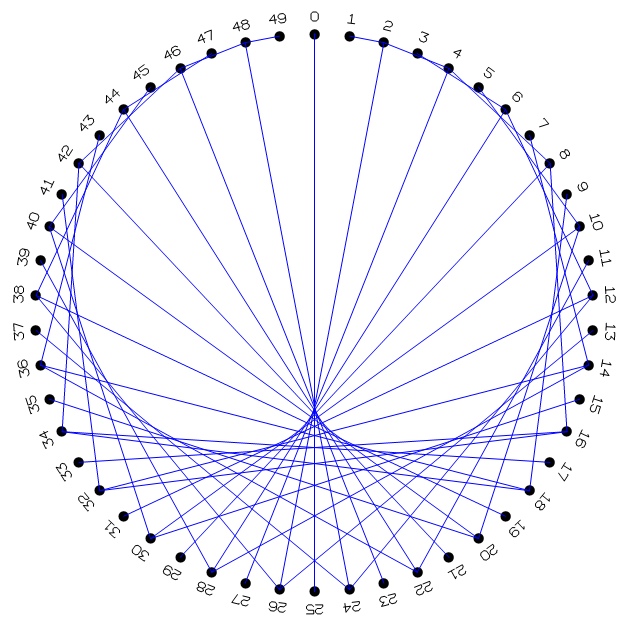 In some classes, time was short so I went on to the next drawing. I distributed circles of 50 dots. This time, rather than addition, we would multiply. Connect 1 to 2, 2 to 4, 3 to 6, and, generally, dot i to dot 2i. Modular arithmetic again is an issue, so I reminded them. What is 2 times 24? 48. What is 2 times 25? 50. But we don't have a 50, so where do we go? 0. I continued for a few more to make sure most of the students understood. I wrote the examples on the board, for later refreshers.
In some classes, time was short so I went on to the next drawing. I distributed circles of 50 dots. This time, rather than addition, we would multiply. Connect 1 to 2, 2 to 4, 3 to 6, and, generally, dot i to dot 2i. Modular arithmetic again is an issue, so I reminded them. What is 2 times 24? 48. What is 2 times 25? 50. But we don't have a 50, so where do we go? 0. I continued for a few more to make sure most of the students understood. I wrote the examples on the board, for later refreshers.
I circulated, helping students. As the figure developed I asked students how they would describe the shape. Many of them said it looks like a heart. I agreed, and told them the math word for it -- cardioid. Most of the students nodded in recognition, saying, "Oh, like cardio?" I selected a few students and gave them a 100 dot circle, and told them to map i --> 3i.
Errors. There were very few errors. Students had gotten used to the rhythm of connecting dot to dot, and calculating. Not a few of my students still lack fluency in calculations such as "times two" but with time it was not beyond them. I was intrigued that, I view this sort of problem a "productive struggle," and think it is beneficial to let students spend time figuring the answer. But my Assistant Principal was in the room for one of the classes, and he gave the answers to a student who was struggling. I saw that she was just completing the calculation on her notebook, correctly, when he told her the answer. Instead of allowing her to feel success, she took his answer and drew the line. I wish he hadn't done that.
In all classes, by this point, I was short on time. But I had made sure that each student was following instructions well enough that they could continue on their own. I asked if anyone wanted a blank paper to do again. Most students asked for this.
I began with a set of Cartesian axes. I provided students with square graph paper and rulers, and instructed them to draw a pair of axes, and the use the ruler in order to make lines as straight as possible. I wanted to axes roughly centered on the paper, but did not instruct so. I knew from experience that most of my students will draw things in the center of a sheet of graph paper, regardless what scale might be appropriate, but I was also counting on some students NOT putting the origin in the center, so we could have a discussion about how that affected our ability to draw the results.
I asked students to name a pair of number that adds to 10, such as 2 and 8. I instructed them to connect 2 on the x-axis to 8 on the y-axis with a straight line. I asked for another pair of numbers, and similarly connect one on the x-axis to the other on the y-axis. I repeated a few times, and the asked students to connect every such pair of numbers they could think of. I waited for students to ask, "How about 0 and 10?" I asked if 0 plus 10 equals 10? Yes. What does it look like when I draw the 0-10 line? Nothing because it's on the axis. So, the full answer is, yes we can use 0-10, but it doesn't add to our figure because it lies on an axis. I similarly waited for students to ask about negative numbers. I asked if there was something we could add to negative 2 that sums to 10. "Yes, positive 12." So we can draw it. In all classes these questions eventually came out. If they had not, I would have asked them, but wanted to wait for students to generate them if possible.
 Errors. Many students in the first class connected to two axis values with big looping curves, despite the instruction to use the ruler to make the line as straight as possible, and despite my modeling this on the board up front. A few students, instead of drawing lines, marked the points whose coordinates add up to ten. I made sure to model more resolutely in subsequent periods, and circulated more busily between groups of desks.
Errors. Many students in the first class connected to two axis values with big looping curves, despite the instruction to use the ruler to make the line as straight as possible, and despite my modeling this on the board up front. A few students, instead of drawing lines, marked the points whose coordinates add up to ten. I made sure to model more resolutely in subsequent periods, and circulated more busily between groups of desks.Once there were a few students with enough lines drawn to discern a shape, I held one up, and asked the class what they though would form as they continued drawing lines. The actual answer is parabola, but no student came up with this. Some students were convinced it would form a circle. I did not correct them, but instead suggested they continue to think about it as they added lines.
 But I did not allow much more time on the Cartesian graph. My main point was to work with circles of numbered points. I distributed copies of 30-dot circles, as shown. Asked what they noticed about the circles. I want to elicit how many dots there are, what the smallest number is, and what the largest number is. Before proceeding, I wanted to make sure they realize that this is one of the cases where we start counting at zero.
But I did not allow much more time on the Cartesian graph. My main point was to work with circles of numbered points. I distributed copies of 30-dot circles, as shown. Asked what they noticed about the circles. I want to elicit how many dots there are, what the smallest number is, and what the largest number is. Before proceeding, I wanted to make sure they realize that this is one of the cases where we start counting at zero.I began by discussing "clock arithmetic." I tried using the more mathematical term, modular arithmetic, but each class clearly preferred "clock," so I went back to that. We tried examples until I was confident they knew how to continue around the circle once they reached the highest number.
 I asked students to choose a number between 1 and 30. (One student chose 15, to interesting result.) Then I instructed they connect each dot, via straight line, to the dot that was their number higher. If they chose 10, they would connect 0 to 10, 1 to 11, 2 to 12, and so on. I reconfirmed they understood modulo. Where would 19 connect? 29. How about 20? 30. But we don't have a 30, so where do we go instead. Oh.
I asked students to choose a number between 1 and 30. (One student chose 15, to interesting result.) Then I instructed they connect each dot, via straight line, to the dot that was their number higher. If they chose 10, they would connect 0 to 10, 1 to 11, 2 to 12, and so on. I reconfirmed they understood modulo. Where would 19 connect? 29. How about 20? 30. But we don't have a 30, so where do we go instead. Oh.I instructed them to continue until all numbered dots have been connected. The figure shows what it would look like if their chosen number were 10. Again, I asked how they would describe the shape they had made. But I had a few students with different numbers hold up their drawings. How are they different. A conjecture formed that "the larger the number, the smaller the circle. In some classes students had chose numbers larger than 15, so I was able to challenge the conjecture, and students struggled to explain that behavior. In the class with a student who chose 15 as her number, all lines intersected at a point in the center, and I asked students if that fit with their conjecture.
Errors. Some students had difficulty understanding the mapping idea, and kept connecting the same dot over and over again to different places on the circle. In the first period, I wrote the numbers as ordered pairs, which may have added to that confusion. From then on, I wrote the pairs with an arrow between (e.g. 1-->11, 4-->14), to emphasize the mapping. I had fewer errors with this notation, but still had to correct a few students.
Some students didn't understand that each of the 30 dots had to be the origin of a connecting line, and each had to be the terminal of a connecting line. At the end there should be two lines for each point. These students stopped early, saying they were done. I showed them how to continue, covering all their dots.
Depending on timing, I went two directions from here. If there was time, and for students who finished quickly, I suggested they choose another number, and with a different color pen they repeat the process.
 In some classes, time was short so I went on to the next drawing. I distributed circles of 50 dots. This time, rather than addition, we would multiply. Connect 1 to 2, 2 to 4, 3 to 6, and, generally, dot i to dot 2i. Modular arithmetic again is an issue, so I reminded them. What is 2 times 24? 48. What is 2 times 25? 50. But we don't have a 50, so where do we go? 0. I continued for a few more to make sure most of the students understood. I wrote the examples on the board, for later refreshers.
In some classes, time was short so I went on to the next drawing. I distributed circles of 50 dots. This time, rather than addition, we would multiply. Connect 1 to 2, 2 to 4, 3 to 6, and, generally, dot i to dot 2i. Modular arithmetic again is an issue, so I reminded them. What is 2 times 24? 48. What is 2 times 25? 50. But we don't have a 50, so where do we go? 0. I continued for a few more to make sure most of the students understood. I wrote the examples on the board, for later refreshers.I circulated, helping students. As the figure developed I asked students how they would describe the shape. Many of them said it looks like a heart. I agreed, and told them the math word for it -- cardioid. Most of the students nodded in recognition, saying, "Oh, like cardio?" I selected a few students and gave them a 100 dot circle, and told them to map i --> 3i.
Errors. There were very few errors. Students had gotten used to the rhythm of connecting dot to dot, and calculating. Not a few of my students still lack fluency in calculations such as "times two" but with time it was not beyond them. I was intrigued that, I view this sort of problem a "productive struggle," and think it is beneficial to let students spend time figuring the answer. But my Assistant Principal was in the room for one of the classes, and he gave the answers to a student who was struggling. I saw that she was just completing the calculation on her notebook, correctly, when he told her the answer. Instead of allowing her to feel success, she took his answer and drew the line. I wish he hadn't done that.
In all classes, by this point, I was short on time. But I had made sure that each student was following instructions well enough that they could continue on their own. I asked if anyone wanted a blank paper to do again. Most students asked for this.