Among the problems we looked at, one in particular intrigued me.
The figure shows three "trains" made up of paired equilateral triangles. The first figure can be thought of as a single pair, the second as two pairs, and the third as three pairs. Students can generate a number of questions on their own about these figures, but eventually lead them to the question, "What is the measure of the long diagonal in each figure."
All the ways I know to answer this question depend on knowing that the altitude of an equilateral triangle is half the length of a side times square root of 3.
Spoiler alert: my discussion of this problem will involve discussing solutions and approaches. If you want to solve on your own, do not read further until you've satisfied yourself. And if that described you, I hope you aren't satisfied until you find a way to solve for the general case of any number of pairs.
where s is the length of a side. For ease of calculation, we will define our unit of measurement to be the same as the length of a side of a single triangle. Hence, unit equilateral triangles, and s = 1.
I presented the drawing to three of my classes on a day when testing was otherwise going to put things out of synch. All of the classes are called "Algebra II" but they perform at very disparate levels. I was not confident that they would remember special right triangles, so I began all three classes with two reminder problems.
Given a right triangle with sides measuring 5 units and 12 units, what is the length of the hypotenuse? This was intended to remind students of the Pythagorean theorem.
What is the height of a unit equilateral triangle? This was intended to remind students of side lengths in 30-60-90 triangles. As I spoke, I noticed that I sometimes switched in "altitude" rather than "height." I decided not to worry about it.
*** edit 21 May 2017 ***
I've decided I should NOT say altitude, as altitude relates to specific segments in a triangle. I drew the auxiliary line off to the side, as height, so as not to give extra hints. By using "altitude" I would somewhat undermine that effort.
*** end edit ***
I was surprised that two students used trigonometry to solve this one. sin(60°). I wonder if they would normally do this, or if it was influenced by EngageNY, which creates a strong association between "height" and "sine."
After these warm ups I presented the drawing of the three "trains." In discussing my classes, I mentioned that I labeled the trains, and I don't recall whether I said figure 1, 2, 3 or n=1, 2, 3. Betina pointed out, and I agree, that one should avoid the "n=" notation, as it boxes students in to one way of thinking in a way that "figure" doesn't. I currently think that no labels at all may be best, to leave it as open as possible.
Introducing the situation, I added a dotting line indicating the diagonal in the first "train." I had equilateral triangle graph paper ready, and offered it to students if they wanted. Some students, seemingly as a reflex action, started shouting out numbers. "1." "2." "1.5." My response to each was, "How do you know? Can you justify that answer?"
For the most part, they settled into group work. The room is arranged with desks in fours.
Interesting wrong answers for first "train": sqrt(6)/2. Students are unfamiliar with adding radicals.
Correct answer: sqrt(3)
*** edit 5/21/2017 ***
These students noticed that the altitudes of the two triangles in the pair lined up. So they added. I didn't see any student multiply by 2. Addition is the prefered operation. Some students, using addition, got to (2*sqrt(3))/2 but did not think to simplify the fraction.
This solution works, but does not generalize because the altitudes don't line up in subsequent trains.
*** end edit ***
Once students got the first train, I suggested finding the diagonal for the second, adding the dotted line diagonal to the second figure. Only two groups in one class and one group in another class got this far.
Interesting wrong answer for second train: 2*sqrt(3). Students assumed it's twice as long as the first diagonal. I added the two single-pair diagonals to the second figure, and asked if they think the new diagonal was the same length as those two put together. Students quickly realized that wasn't the answer, and went back to puzzling.
The period ended before anyone got the correct answer, sqrt(7). Correct answer for third train is sqrt(13). Correct answer for the nth train is sqrt(n^2+n+1).
*** edit 5/21/2017 ***
The solution I found was to draw in another "half" triangle at the end of the train. This creates an obvious right triangle with side lengths n+1/2 and sqrt(3)/2. Application of the Pythagorean theorem, with the opportunity for work with squaring a binomial involving a fraction, gives the general solution.
*** end edit ***
All in all, I was very pleased with the level of engagement most students showed. It was something they were curious about, and they felt they should have enough math knowledge to do it. I even noted that one chronic attendance problem student happened to come that day, and even he got into the problem. He never got past working on the altitude of the triangle, but that threshold was low enough that he felt comfortable diving in. Additionally, the ceiling was high enough, none of the students exhausted the potential of the problem. If they had figured the nth case, I could follow with how long is the shorter diagonal? What if I configured the trains in different ways. This is a very rich problem.

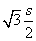


This is great!! I like the way you push the low ceiling/high ceiling threshold to make it very specific and relevant to all students.
ReplyDeleteThanks for sharing the blog with me. Not only do I enjoy your tone and curiosity, but I know if I read it regularly and try the math, I will learn a thing or two!
ReplyDelete-Courtney
Very much like this problem. It only requires pythagorean theorem, although 30-60-90 triangle is helpful. Given enough time, students can find pattern for length of nth diagonal, especially if they have studied sequences. Thanks!
ReplyDelete