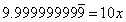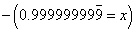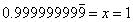Over Thanksgiving dinner we were discussing a calculation that had come up, and my wife (born and raised in Japan) commented that it was a "tsuru-kame (crane and turtle)" situation. My son and I, both puzzled, asked for an explanation of what a crane and turtle situation was. My wife was surprised I had never heard of it, and proceeded to try to explain the calculation algorithm. Unfortunately, too many years had intervened between her middle school, where she learned the technique, and the dinner, and she couldn't quite explain.
So we all looked it up later, and I, in the process, learned some interesting cultural tidbits, and also learned another algorithm for solving what I call coin problems. You've got some number of things with one value associated, and some number with another value, know the total number of things, and know the total value. Find the number of each item.
This is a typical lesson in New York's Algebra curriculum. It appeared in Integrated Algebra, Math A before that, and, I assume, in whatever name they gave Algebra before Math A. I assume it's in CCLS Algebra, as well. We teach to solve using the technique of simultaneous equations and substitution.
The Tsuru-Kame method (鶴亀) takes a different approach that seems more like using area to solve.
Let's pretend we have a bunch of cranes and turtles, totaling 10 animals. Let's also say that there are 34 legs all together in this menagerie. Cranes each have two legs, and turtles have four. So the difference between them is two legs. If we were to assume all the animals are turtles, we'd come up with 40 legs. This is six extra legs than we actually have. Divide that six by the difference between crane and turtle leg count (2) and we get three. So that is the number of cranes. Which means there must have been seven turtles. (Check: 3 cranes @ 2 legs is 6 legs, 7 turtles @ 4 legs is 28 legs, for a total of 34 legs. It works.)
This method avoids algebra, but is pretty intriguing to me. I am almost always happy to learn a new algorithm.
I was a public school teacher in New York City for over 16 years. Then I taught mathematics at an international school in Frankfurt am Main, Germany. Now I'm mostly retired but still teach a few class each year at Purchase College. This blog is intended as a spot for me to record some of my observations.
Sunday, November 30, 2014
Thursday, September 4, 2014
Twelfth Period
Back in June we were given our tentative teaching programs, and I was intrigued to see that I was assigned a Robotics class. Although I've played with Lego Mindstorms, I've never received any formal training in robotics. But I thought with a little support I could do this.
Through discussions with my Assistant Principal, and some outside help from a fellow who has helped set up similar programs in schools, we initially thought of using Mindstorm EV3. The weakness with the Lego is that students associate it with younger kids, and some of them tune out.
So, during the summer I wasn't too surprised to find that they had switched platforms to something called BoeBot sold by Parallax. I was sent a sample curriculum, and some ideas for working with the kits, and I began doing research, but also confirming that I would receive training.
The next day I was told that they had switched platforms again. This time it would be something called Vex with a curriculum from Intellitek. Fine. I don't care. I don't know anything about any of them, so as long as I receive training I will do whatever they buy.
Today was the first day of school. They still haven't decided for sure just what platform I'm to base this Robotics class on. I am still not scheduled for training in anything. But to keep things really interesting, my class has been split. I have half of the students during 8th period, as my fifth teaching period of the day.
The other half, it appears, have been scheduled to meet with me 12th period. Twelfth! We don't even have a 12th period. I have no idea what time it would meet if I were to try to show up for it. I'm told that some of the 12th period students came to the classroom during 9th period, but I wasn't there. I only teach 1-8, and was taking care of paperwork during 9th period.
(I've also heard that administrators at my school have scheduled a meeting next week with some people to decide what platform I should be using in my class. Which started already. In case I didn't emphasize that already. That it's really late to be making these decisions. And why not just use that last one I heard about in the summer.)
Through discussions with my Assistant Principal, and some outside help from a fellow who has helped set up similar programs in schools, we initially thought of using Mindstorm EV3. The weakness with the Lego is that students associate it with younger kids, and some of them tune out.
So, during the summer I wasn't too surprised to find that they had switched platforms to something called BoeBot sold by Parallax. I was sent a sample curriculum, and some ideas for working with the kits, and I began doing research, but also confirming that I would receive training.
The next day I was told that they had switched platforms again. This time it would be something called Vex with a curriculum from Intellitek. Fine. I don't care. I don't know anything about any of them, so as long as I receive training I will do whatever they buy.
Today was the first day of school. They still haven't decided for sure just what platform I'm to base this Robotics class on. I am still not scheduled for training in anything. But to keep things really interesting, my class has been split. I have half of the students during 8th period, as my fifth teaching period of the day.
The other half, it appears, have been scheduled to meet with me 12th period. Twelfth! We don't even have a 12th period. I have no idea what time it would meet if I were to try to show up for it. I'm told that some of the 12th period students came to the classroom during 9th period, but I wasn't there. I only teach 1-8, and was taking care of paperwork during 9th period.
(I've also heard that administrators at my school have scheduled a meeting next week with some people to decide what platform I should be using in my class. Which started already. In case I didn't emphasize that already. That it's really late to be making these decisions. And why not just use that last one I heard about in the summer.)
Tuesday, June 10, 2014
Leaving for Kansas City
For the first time, I've been invited by Education Testing Service to join in the grading (called "reading") of AP Calculus exams. So I'm heading off to Kansas City for a week to sit with hundreds of other math teachers and read AP Calculus exams from around the world.
I think this is very cool, and I'm really looking forward to it.
I think this is very cool, and I'm really looking forward to it.
Sunday, June 1, 2014
Sometimes I Think They Don't Know English
Following are excerpts from a student responses on a geometry quiz about locus.
The locus of points is the radius of a circle of 2 units
The locus of points is a parallel line radius = 2
The two points are equidistant from each other
The locus is the center with a radius of 3
The locus is a line bisector
The lines are parallel and the locus is their angle bisector
The locus is equidistant and parallel lines. and maybe a circle. maybe.
The locus is two circles that intercept
Point A is the center of a circle with all points equidistant by four units
Two lines cut two points connected by a 2 units line from the midpoint of the 6 unit long line
The locus of points is the perpendicular bisector of the angle
The locus of point is a parallel line line of the segment
I used the midpoint formula to find the locus and it is equidistant from 2 units of (2, 4)
The lines are parallel from the distance
The loci is the midpoint of two equidistant lines that have two points
Rise over run
The locus of points is the radius of a circle of 2 units
The locus of points is a parallel line radius = 2
The two points are equidistant from each other
The locus is the center with a radius of 3
The locus is a line bisector
The lines are parallel and the locus is their angle bisector
The locus is equidistant and parallel lines. and maybe a circle. maybe.
The locus is two circles that intercept
Point A is the center of a circle with all points equidistant by four units
Two lines cut two points connected by a 2 units line from the midpoint of the 6 unit long line
The locus of points is the perpendicular bisector of the angle
The locus of point is a parallel line line of the segment
I used the midpoint formula to find the locus and it is equidistant from 2 units of (2, 4)
The lines are parallel from the distance
The loci is the midpoint of two equidistant lines that have two points
Rise over run
Tuesday, May 20, 2014
Game Piece
My colleague, Ms. Luna, has assigned her AP Calculus students a year-end project. They are, in groups, to create a game, based on some board game they already know, but with a Calculus theme. I enter the picture because these students imagine that they can come to me and simply say "print me something like a game piece," and I'll immediately be able to fire up my 3D printer and print out exactly the piece they are imagining. When I try to get them involved in actually designing whatever it is they want, they usually turn and walk away.
This morning I had a student, N, who was willing to work on design. (right there, it makes me happy) So we sat together and I tried to get N to give me her specifications. I tried, bit by bit, to nudge her towards speaking in terms of geometric solids.
I eventually got N to describe the game piece as a cube with a sphere sitting on top. We drafted the idea of the cube as the intersection of inequalities in the x, y, and z directions. Equation of a sphere is standard, and wasn't a problem once we decided radius and how much it should overlap the cube. From there I was able to work on designing in Mathematica. We wound up with
RegionPlot3D[Abs[x] < 1/2 && Abs[y] < 1/2 && Abs[z] < 1/2 || Sqrt[x^2 + y^2 + (z - 5/8)^2] < (5/8)^2, {x, -1, 1}, {y, -1, 1}, {z, -1, 2}, PlotPoints -> 50, BoxRatios -> Automatic]
I exported the plot to .stl, and opened the file in MakerWare. As usual, MakerWare wanted me to scale the drawing. She wanted two game pieces, so I copied the scaled piece a little to the right. Lately I've been printing almost everything with a raft, so I selected the raft option, reduced the solid fill to 7% (default was 10%), and clicked print.
Printing went fine. I was about to break off the raft when N stopped me. "No! I like that!" Okay by me.
This morning I had a student, N, who was willing to work on design. (right there, it makes me happy) So we sat together and I tried to get N to give me her specifications. I tried, bit by bit, to nudge her towards speaking in terms of geometric solids.
I eventually got N to describe the game piece as a cube with a sphere sitting on top. We drafted the idea of the cube as the intersection of inequalities in the x, y, and z directions. Equation of a sphere is standard, and wasn't a problem once we decided radius and how much it should overlap the cube. From there I was able to work on designing in Mathematica. We wound up with
RegionPlot3D[Abs[x] < 1/2 && Abs[y] < 1/2 && Abs[z] < 1/2 || Sqrt[x^2 + y^2 + (z - 5/8)^2] < (5/8)^2, {x, -1, 1}, {y, -1, 1}, {z, -1, 2}, PlotPoints -> 50, BoxRatios -> Automatic]
I exported the plot to .stl, and opened the file in MakerWare. As usual, MakerWare wanted me to scale the drawing. She wanted two game pieces, so I copied the scaled piece a little to the right. Lately I've been printing almost everything with a raft, so I selected the raft option, reduced the solid fill to 7% (default was 10%), and clicked print.
Printing went fine. I was about to break off the raft when N stopped me. "No! I like that!" Okay by me.
Wednesday, April 16, 2014
Lissajous
Finally, I've got some moderate success to report with my Lissajous figure.
Yesterday I tried printing with raft and supports (because of printing difficulties without).
So the figure printed, although it took a long time (a little over two hours) because extruding all the extra plastic for the supports was a significant addition. Then, afterwards, the supports needed to be broken out.
And that's where the issues arose. Even though I repaired the .stl file with visCAM and netfabb, the intersections points were still weak, and I could see light coming through them. They didn't appear to be solid connections. The physical stress of breaking off the supports was more than the structure could deal with, and it began to break. "Don't worry," people told me, "you can superglue it back together." But that's not the point. I wanted to print as a single piece.
I thought of taking the piece home and use my Dremel rotary tool to get the rest of the supports off. But I left school in a hurry, and neglected to pack it.
While doing whatever it is I do when not at work, an idea came to me -- rotate the figure 90 degrees in the y-z plane. The problem had been my horizontal spans had been too long, but by rotating I'd change those horizontals to verticals. Verticals don't typically have as much issue printing.
So that's what I tried this morning. Using the exact same .stl file, I used MakerWare to rotate, and printed with rafts but without supports. Success!
If anyone wants, here's the .thing on thingiverse.
*** change history ***
4/19/2014 added link to .thing file
4/16/2014 corrected spelling
Yesterday I tried printing with raft and supports (because of printing difficulties without).
 |
| somehow reminds me of the World Series trophy |
 |
| removing supports with my handy dandy leatherman tool |
 |
| printed with supports, mostly removed, but lost integrity of the plot in the process |
While doing whatever it is I do when not at work, an idea came to me -- rotate the figure 90 degrees in the y-z plane. The problem had been my horizontal spans had been too long, but by rotating I'd change those horizontals to verticals. Verticals don't typically have as much issue printing.
So that's what I tried this morning. Using the exact same .stl file, I used MakerWare to rotate, and printed with rafts but without supports. Success!
 |
| small raft under each loop |
 |
| printing complete. I like the wisp of PLA trailing back to the print head. |
 |
| before removing the rafts |
 |
| after removing the rafts. hand modeling courtesy of Eloise. |
*** change history ***
4/19/2014 added link to .thing file
4/16/2014 corrected spelling
Saturday, April 12, 2014
Fixing 3D Designs
One of the things George warned us about is the possiblity that Mathematica might create an invalid .stl file when it exports. I don't understand the bug exactly, but somehow when it draws the .stl, which is composed of many triangles which have orientation, it might create some triangles either with orientation reversed, or with edges that don't align correctly. He suggested two tools to detect and fix these errors.
Since I had a problem printing my lissajous figure (see image below), I thought it might be from this sort of error. I downloaded and installed the first tool, VisCam, and it indeed found 24 flipped triangles. But this tool cannot fix. It can only check for errors. So I downloaded and installed the second tool, NetFabb. It took a while for me to figure this one out, but eventually I found the menu to check, and the menu to repair errors. But it wants to save only in its own format, and it took me a while to discover how to export back to .stl. Turns out the part has to be selected for this option to appear. Okay, obvious, but it took me a while.
Next week I'll try printing the repaired part, and I'll report back on how it goes.
Since I had a problem printing my lissajous figure (see image below), I thought it might be from this sort of error. I downloaded and installed the first tool, VisCam, and it indeed found 24 flipped triangles. But this tool cannot fix. It can only check for errors. So I downloaded and installed the second tool, NetFabb. It took a while for me to figure this one out, but eventually I found the menu to check, and the menu to repair errors. But it wants to save only in its own format, and it took me a while to discover how to export back to .stl. Turns out the part has to be selected for this option to appear. Okay, obvious, but it took me a while.
Sunday, April 6, 2014
Infinite Series
Sometimes the amazed reaction of a student becomes the high point of a day or week.
Discussing series in Calculus class, and one student brings up the example of how
They've obviously heard this one before, but one student up front mutters, "They say that, but I don't see how it's possible." I think I first saw this proof back in 8th grade, from my then teacher Eugene Thompson. I think the idea of converting repeating decimals to fractions was part of the curriculum, and I never checked if that's still something in the middle school standards.
But I offered, "I can prove it pretty quickly to you, if you like." Over half the class nodded and vocalized assent. Perhaps nobody has every bothered to show them this. So I began (most of my math friends know these steps, so bear with me).
I checked, and everyone was okay with this step. So I continued.
Again, I checked. Everybody was okay this this step. So I said I would subtract the first from the second
A third time, I paused and confirm everybody was okay with my steps. No funny business.
This is the result of the subtraction. Still very straightforward. Of course, next I divide both sides by 9.
"Whoa! Wait a second! How did that happen?" A student in back who wasn't paying attention asked me to do it again. Another student asked if it always works (by which I think she meant does that work for all repeating decimals). So I showed them again with 0.6666 repeating. I had them amazed and enthralled.
It was a ten minute diversion in a 98 minute class. I think it was worth it.
Discussing series in Calculus class, and one student brings up the example of how
They've obviously heard this one before, but one student up front mutters, "They say that, but I don't see how it's possible." I think I first saw this proof back in 8th grade, from my then teacher Eugene Thompson. I think the idea of converting repeating decimals to fractions was part of the curriculum, and I never checked if that's still something in the middle school standards.
But I offered, "I can prove it pretty quickly to you, if you like." Over half the class nodded and vocalized assent. Perhaps nobody has every bothered to show them this. So I began (most of my math friends know these steps, so bear with me).
I checked, and everyone was okay with this step. So I continued.
Again, I checked. Everybody was okay this this step. So I said I would subtract the first from the second
A third time, I paused and confirm everybody was okay with my steps. No funny business.
This is the result of the subtraction. Still very straightforward. Of course, next I divide both sides by 9.
"Whoa! Wait a second! How did that happen?" A student in back who wasn't paying attention asked me to do it again. Another student asked if it always works (by which I think she meant does that work for all repeating decimals). So I showed them again with 0.6666 repeating. I had them amazed and enthralled.
It was a ten minute diversion in a 98 minute class. I think it was worth it.
Friday, April 4, 2014
Checksums for Groupwork
I was trying to refresh my memory of what Jill Gough has showed me about leveled assessments, and so I was searching her blog Experiments in Learning by Doing. In that process, I came across a link she had to this post from Function of Time, blogged by Kate Nowak. I was intrigued by the idea, and decided to try to adapt it to my classroom.
I teach three sections of Geometry this year, one freshmen and two sophomore. I chose to write an activity for Distance Formula using this self-check routine. With the help of my awesome student teacher, this year I've managed to make meaningful groupwork the norm in my classroom. So the students are used to a lot of the typical classroom rules of groupwork (ask each other before asking teacher, work with your own group rather than others, etc). I wouldn't recommend trying this on the first day of groups.
We've spent a few days applying Pythagorean theorem to triangle problems. The next task in our pacing calendar is to draw the tie to distance formula. I introduced the idea with a brief explanation showing we can calculate distance between points not on the same vertical or horizontal line by making those points endpoints of a segment corresponding to the hypotenuse of a right triangle whose legs are horizontal and vertical. I try to emphasize that the distance formula, littered with subscripts and pesky subtractions and additions and exponents and radicals, is really just the Pythagorean theorem, which my students all knew before they ever met me.
So, we worked a few problems together. Then I let them loose with their worksheets.
As Ms. Nowak describes, I had groupings of four students, four worksheets of graduated difficulty on differently colored paper, the colors posted in order on the board, with the checksum folded inside.
I gave the verbal instructions, as this task is a little different than other group tasks we've done. Each student is to do one problem per sheet. I asked them to write their name next to the problem they worked. When all four problems are finished, add the numerical answers and check it against the checksum on the whiteboard. My classroom calculators were made available to students who don't carry their own.
The orange and blue sheets had straightforward distance problems; orange with integers and blue with radicals. The green sheet gave distances and three of four coordinates, asking for the missing coordinate. The yellow sheet gave vertices of polygons and asked things about the underlying polygons.
Things didn't go so well for the first class. I noticed almost all groups started with the yellow (most difficult) sheet, and didn't make any progress. My suggestion they start with the orange (easier) met few results. When the period bell rang, no group had completed any entire single sheet.
For the second class, I began by only distributing the orange and blue sheets. As groups made progress, I gave them the green, and then the yellow. The second class is my freshmen (ninth grade) who typically have difficulty focusing on work. Even so, they made much better progress than the first group. I used the same distribution pattern for the third class, and they did the most work of all. Almost all the groups at least began work on the last sheet.
I really like the self-reliance aspect of this idea, and will use it again for future lessons. (My paper is Wausau Astrobrights, which I love.)
*** edit 6 April 2014 ***
a link to the worksheets I used
I teach three sections of Geometry this year, one freshmen and two sophomore. I chose to write an activity for Distance Formula using this self-check routine. With the help of my awesome student teacher, this year I've managed to make meaningful groupwork the norm in my classroom. So the students are used to a lot of the typical classroom rules of groupwork (ask each other before asking teacher, work with your own group rather than others, etc). I wouldn't recommend trying this on the first day of groups.
We've spent a few days applying Pythagorean theorem to triangle problems. The next task in our pacing calendar is to draw the tie to distance formula. I introduced the idea with a brief explanation showing we can calculate distance between points not on the same vertical or horizontal line by making those points endpoints of a segment corresponding to the hypotenuse of a right triangle whose legs are horizontal and vertical. I try to emphasize that the distance formula, littered with subscripts and pesky subtractions and additions and exponents and radicals, is really just the Pythagorean theorem, which my students all knew before they ever met me.
So, we worked a few problems together. Then I let them loose with their worksheets.
As Ms. Nowak describes, I had groupings of four students, four worksheets of graduated difficulty on differently colored paper, the colors posted in order on the board, with the checksum folded inside.
I gave the verbal instructions, as this task is a little different than other group tasks we've done. Each student is to do one problem per sheet. I asked them to write their name next to the problem they worked. When all four problems are finished, add the numerical answers and check it against the checksum on the whiteboard. My classroom calculators were made available to students who don't carry their own.
The orange and blue sheets had straightforward distance problems; orange with integers and blue with radicals. The green sheet gave distances and three of four coordinates, asking for the missing coordinate. The yellow sheet gave vertices of polygons and asked things about the underlying polygons.
Things didn't go so well for the first class. I noticed almost all groups started with the yellow (most difficult) sheet, and didn't make any progress. My suggestion they start with the orange (easier) met few results. When the period bell rang, no group had completed any entire single sheet.
For the second class, I began by only distributing the orange and blue sheets. As groups made progress, I gave them the green, and then the yellow. The second class is my freshmen (ninth grade) who typically have difficulty focusing on work. Even so, they made much better progress than the first group. I used the same distribution pattern for the third class, and they did the most work of all. Almost all the groups at least began work on the last sheet.
I really like the self-reliance aspect of this idea, and will use it again for future lessons. (My paper is Wausau Astrobrights, which I love.)
*** edit 6 April 2014 ***
a link to the worksheets I used
Tuesday, March 25, 2014
Printing 25 March 2014 (and Egg Holder POC)
Printing the cube was uneventful until the top cross-edges. I was intrigued to note that the PLA bridged the uprights perfectly in the front-back direction, but drooped in the left-right direction. At first I was dismayed, but then I realized it looked interesting, and let the job continue. After a few layers the software shifted direction, and laid down enough support that the drooping spaghetti effect stopped. I'm interested that this happened in one direction only, and, since the faces of a cube should be congruent, wonder why it happened.
Although the photos below show the thing on my print platform, it's after I've lifted it from the plate, and rotated to try to get a good photo. (Canon PowerShot SD970 IS in macro focus mode)
Although my egg holder finished plotting earlier, the cube took over 50 minutes to print, so I didn't have a lot of time left for that. Basically, the function was a sum of sine curves in the x and y directions. Function call was
RegionPlot3D[ Abs[z - (Sin[2*x] + Sin[2*y])] < .1, {x, -3*Pi, 3*Pi}, {y, -3*Pi, 3*Pi}, {z, -3, 3}]
There were a lot of holes in my surface, so I had to step up PlotPoints. Each tick up increases the calculation time for the RegionPlot, but at each increase there were still holes. It wasn't until I got to PlotPoints->300 that the surface looked smooth and continuous. But took forever to calculate.
Time was short, so I decided to try printing as the .stl from Mathematica loaded in MakerWare, which is tiny because of the scaling issues with the .stl format. But, as I was warned, doubling the size would roughly octuple the print time, since it would multiply the volume of plastic used eight-fold.
Print was obviously failing from the start. It wasn't sticking to the print platform. So I cancelled the job, and tried again with a raft. This print was successful, even if ridiculously tiny. But it serves as a proof of concept. That is, my sinusoidal egg holder is a viable design. When I have time, I'll try the printout again at double size. Since this tiny one took just over ten minutes, a double size should take under an hour and a half.
Friday, March 21, 2014
3D Printing Friday March 21
This would be much more convenient if I had a secure place to leave my printer. But I have to lock it in a cabinet, and I really only can work with it after school. So today I decided to stay late and try to print.
One issue last time was the thing didn't stick to the print plate. I've found this comes from two causes. To remedy one, I covered the print plate with blue painter tape. This will also help release the finished thing from the print plate, which has been a problem in the past.
I tried printing again, and as the MakerWare software was slicing my thing (the egg holder) I realized another problem. I have edges floating in space. Duh! Of course that won't print well. I need to design a frame around the thing, or else print with supports.
Once the print started, even before it got to the point of hanging objects, I could tell the print wasn't going well. The print still wasn't sticking to the plate. The way it was coming loose, I think, is associated with the plate being out of level. So I canceled the print job in order to level.
As easy as it is in theory to level the plate, it isn't a precise science. The instructions say "raise the plate until you feel just a little friction between the print head and the plate." There's a lot of room for interpretation in that instruction. So I decided to try something that I know I've had success with in the past, and keep trying until it came out good again. That was the five link chain that comes preloaded on the SD card with the printer. After three tries, it printed perfectly.
By this time, it was already 4:30, and I was tired. I wanted at least one nice thing, and didn't want to experiment with my own bad design again. I went to thingiverse and did a search under "hart" to see if I could find any George Hart designs. Sure enough, there are a few available. I selected an open dodecahedron sculpture, downloaded, and sent to the printer. It took almost an hour, but I did end the day with a lovely dodecahedron to show for my efforts (even if it wasn't my own design).
I'll work more on my egg holder this weekend, and, if I have time, try to print during the day Monday.
One issue last time was the thing didn't stick to the print plate. I've found this comes from two causes. To remedy one, I covered the print plate with blue painter tape. This will also help release the finished thing from the print plate, which has been a problem in the past.
I tried printing again, and as the MakerWare software was slicing my thing (the egg holder) I realized another problem. I have edges floating in space. Duh! Of course that won't print well. I need to design a frame around the thing, or else print with supports.
Once the print started, even before it got to the point of hanging objects, I could tell the print wasn't going well. The print still wasn't sticking to the plate. The way it was coming loose, I think, is associated with the plate being out of level. So I canceled the print job in order to level.
As easy as it is in theory to level the plate, it isn't a precise science. The instructions say "raise the plate until you feel just a little friction between the print head and the plate." There's a lot of room for interpretation in that instruction. So I decided to try something that I know I've had success with in the past, and keep trying until it came out good again. That was the five link chain that comes preloaded on the SD card with the printer. After three tries, it printed perfectly.
By this time, it was already 4:30, and I was tired. I wanted at least one nice thing, and didn't want to experiment with my own bad design again. I went to thingiverse and did a search under "hart" to see if I could find any George Hart designs. Sure enough, there are a few available. I selected an open dodecahedron sculpture, downloaded, and sent to the printer. It took almost an hour, but I did end the day with a lovely dodecahedron to show for my efforts (even if it wasn't my own design).
I'll work more on my egg holder this weekend, and, if I have time, try to print during the day Monday.
Wednesday, March 19, 2014
Group Work as the Norm
This semester I am very fortunate to be working with a fantastic Student Teacher. He, also, is with MfA, and he had a full semester with another Cooperating Teacher at different school. He came to me already well at ease in the classroom, with good management skills.
As an MfA member, he goes to workshops periodically, and last week attended one on group work. He asked if he could try some of the techniques in our class. I said sure. Today was the trial.
Before students arrived, desks were arranged in groupings of four, with a group number posted on one of each grouping of desks. Five rules were written on the board.
1) You must make sure each member of your group understands the instructions.
2) Each group member is responsible for answering all questions fully
3) If members of the group disagree on an answer, they must discuss until they come up with a single answer for the group. All group members must be able to explain the group answer.
4) Before you may ask a teacher a question you must ask each of the members of your group to answer the question.
5) You may not talk to members of any other group.
We had a worksheet with a few questions comparing volume and price of donuts versus donut holes, and asked for surface area of a cake with the same volume as a dozen donuts.
I have never seen my students so engaged. All three geometry classes had better than 95% of students actively involved in discussion, sense-making, hypothesis testing, and doing mathematics.
The person who led the workshop apparently says he exclusively does group work. I'm not sure how that works out, as I think there's some material that requires at least a bit of teacher presentation. But I certainly see how this technique could be very effective in my classroom on a frequent basis. I look forward to exploring more with it. The difficulty seems to be in coming up with group projects day after day.
Today was a positive.
As an MfA member, he goes to workshops periodically, and last week attended one on group work. He asked if he could try some of the techniques in our class. I said sure. Today was the trial.
Before students arrived, desks were arranged in groupings of four, with a group number posted on one of each grouping of desks. Five rules were written on the board.
1) You must make sure each member of your group understands the instructions.
2) Each group member is responsible for answering all questions fully
3) If members of the group disagree on an answer, they must discuss until they come up with a single answer for the group. All group members must be able to explain the group answer.
4) Before you may ask a teacher a question you must ask each of the members of your group to answer the question.
5) You may not talk to members of any other group.
We had a worksheet with a few questions comparing volume and price of donuts versus donut holes, and asked for surface area of a cake with the same volume as a dozen donuts.
I have never seen my students so engaged. All three geometry classes had better than 95% of students actively involved in discussion, sense-making, hypothesis testing, and doing mathematics.
The person who led the workshop apparently says he exclusively does group work. I'm not sure how that works out, as I think there's some material that requires at least a bit of teacher presentation. But I certainly see how this technique could be very effective in my classroom on a frequent basis. I look forward to exploring more with it. The difficulty seems to be in coming up with group projects day after day.
Today was a positive.
Tuesday, March 18, 2014
3D Printing part 5
I finally received my new laptop, so I was finally able to install Mathematica with full license. This means I'm able to export to .stl format, which is needed to communicate with MakerWare.
One of the homework assignments from class was to make an "egg carton." I decided to start with an egg holder without lid. Not really a carton, but I figure that's fair since I'm a beginner.
Although I tweaked the parameters a bit, basically my surface is z=sin(x)+sin(y). Mathematica draws it with lots of gaps, so I needed to increase PlotPoints up to 200 before it looked even close to okay. That significantly slowed down the plotting.
Once I had a plot, I exported to .stl. The syntax of the command is Export["filename",whattoexport], which took me a while to figure out, because I was too lazy to look up the help reference. In the end, I would have saved time by looking it up first.
Next I opened the file in MakerWare, which immediately asked permission to put the drawing on the platform. Good call, I thought. It looked really tiny, so I tried scaling it up, and clicked the command to print.
The Replicator 2 makes all sorts of cute noises as it prints. I let it run for a while, but it became clear I wasn't getting good results, I think I need to level the Plexiglas surface. Try again tomorrow.
One of the homework assignments from class was to make an "egg carton." I decided to start with an egg holder without lid. Not really a carton, but I figure that's fair since I'm a beginner.
Although I tweaked the parameters a bit, basically my surface is z=sin(x)+sin(y). Mathematica draws it with lots of gaps, so I needed to increase PlotPoints up to 200 before it looked even close to okay. That significantly slowed down the plotting.
Once I had a plot, I exported to .stl. The syntax of the command is Export["filename",whattoexport], which took me a while to figure out, because I was too lazy to look up the help reference. In the end, I would have saved time by looking it up first.
Next I opened the file in MakerWare, which immediately asked permission to put the drawing on the platform. Good call, I thought. It looked really tiny, so I tried scaling it up, and clicked the command to print.
The Replicator 2 makes all sorts of cute noises as it prints. I let it run for a while, but it became clear I wasn't getting good results, I think I need to level the Plexiglas surface. Try again tomorrow.
Monday, March 17, 2014
Arduino Day 2
Second Arduino workshop. It was a whirlwind, and hard to keep up just typing code.
Learned about Pulse Width Modulation to a digital pin. Wrote a program to fade in and out.
Then worked with a speaker, making noises, which gets old very quickly.
Good fun. I need to redo some of these things on my own, to make sure I really get them.
Learned about Pulse Width Modulation to a digital pin. Wrote a program to fade in and out.
Then worked with a speaker, making noises, which gets old very quickly.
Good fun. I need to redo some of these things on my own, to make sure I really get them.
Sunday, March 16, 2014
Ten County TCMEA Annual Conference Ossining March 2014
I've uploaded key files related to my talk on my website.
Friday, March 14, 2014
Knots
Some time ago I happened upon instructions for a Mathematically Correct Breakfast which involves slicing a bagel in such a way that it forms two linked rings. I practiced the technique, and have since amused myself by showing off whenever given the opportunity.
Fast forward to last Monday when I had my first class in 3D printing with Mathematica and Makerbot Replicator 2. The teacher is George Hart. George Hart is the man who wrote the instructions for the Mathematically Correct Breakfast.
Next stop, this morning, as I followed an acquaintance's Twitter link to a video called Anti-Pi Rant. The video was created by mathemusician, Vi Hart. But wait. Can it be? Vi Hart is George Hart's daughter?
I need to take a break to eat a hexaflexa-burrito.
Fast forward to last Monday when I had my first class in 3D printing with Mathematica and Makerbot Replicator 2. The teacher is George Hart. George Hart is the man who wrote the instructions for the Mathematically Correct Breakfast.
Next stop, this morning, as I followed an acquaintance's Twitter link to a video called Anti-Pi Rant. The video was created by mathemusician, Vi Hart. But wait. Can it be? Vi Hart is George Hart's daughter?
I need to take a break to eat a hexaflexa-burrito.
Tuesday, March 11, 2014
Arguing Angles
I'm working with a group of other Geometry teachers in my school trying to plan lessons together. Monday afternoon we got into a heated discussion. The topic? How to define the major arc of a circle.
We all agreed on the textbook definition of a minor arc: if the measure of the corresponding central angle is less than 180 degrees, then it is a minor arc. But the dispute was about the definition for a major arc.
My colleagues wanted to use parallel language, saying it is the arc for a central angle greater than 180 degrees. But our text has never discussed what it might mean to be greater than 180 degrees. In fact, were we to allow angle measures greater than 180 degrees, then we lose the definitions of "interior" and "exterior" of angles, and consequently a multitude other relationships become ambiguous or wrong.
I'd rather go with our textbook's definition of major arc, which uses the idea of "not interior to the central angle." This maintains the idea of angle being less than (or equal to) 180 degrees, and preserves definitions of interior. But my colleagues say this is too complicated, and our students can't handle it.
My colleagues argued that in Trigonometry we regularly use angles much greater than 180 degrees and much less than 0. But I pointed out that in Trigonometry, in order to go beyond 90 degrees, we must view angles as rotations, while in Geometry they are static. This didn't persuade them.
We regularly have discussions about rigor, and holding our students to high expectations. How can we on one hand water down content and on the other hand say we are rigorously holding high expectations?
We all agreed on the textbook definition of a minor arc: if the measure of the corresponding central angle is less than 180 degrees, then it is a minor arc. But the dispute was about the definition for a major arc.
My colleagues wanted to use parallel language, saying it is the arc for a central angle greater than 180 degrees. But our text has never discussed what it might mean to be greater than 180 degrees. In fact, were we to allow angle measures greater than 180 degrees, then we lose the definitions of "interior" and "exterior" of angles, and consequently a multitude other relationships become ambiguous or wrong.
I'd rather go with our textbook's definition of major arc, which uses the idea of "not interior to the central angle." This maintains the idea of angle being less than (or equal to) 180 degrees, and preserves definitions of interior. But my colleagues say this is too complicated, and our students can't handle it.
My colleagues argued that in Trigonometry we regularly use angles much greater than 180 degrees and much less than 0. But I pointed out that in Trigonometry, in order to go beyond 90 degrees, we must view angles as rotations, while in Geometry they are static. This didn't persuade them.
We regularly have discussions about rigor, and holding our students to high expectations. How can we on one hand water down content and on the other hand say we are rigorously holding high expectations?
Monday, March 10, 2014
Mathematica and Makerware and Replicator 2
Today was the first Math for America mini-course session on 3D Printing, led by George Hart of Stony Brook University. Mostly what I learned is how amazingly easy it is to use Mathematica as a design tool. Essentially, you plot whatever 3D function it is you're working on (RegionPlot3D), and export that plot to an .stl file. Done.
Currently, the biggest issue is that I'm using a trial version of Mathematica, which doesn't allow export. But my new laptop is supposed to arrive in a few days, and I'll install the full version of Mathematica on that. Then I'll be good to go.
My homework: design and print a knob for a rotary light dimmer switch, and design and print a carton for (an unspecified number of) eggs.
Currently, the biggest issue is that I'm using a trial version of Mathematica, which doesn't allow export. But my new laptop is supposed to arrive in a few days, and I'll install the full version of Mathematica on that. Then I'll be good to go.
My homework: design and print a knob for a rotary light dimmer switch, and design and print a carton for (an unspecified number of) eggs.
Tuesday, March 4, 2014
T^3 International Conference
Heading off for the annual conference. This is always a nice event for me as a teacher. On Thursday I conference with other TI Instructors. On Friday and Saturday I get to meet with other math and science teachers from around the world to share practices. Should be a good event.
(I expect my twitter activity will increase dramatically for the next few days).
(I expect my twitter activity will increase dramatically for the next few days).
Tuesday, February 4, 2014
Teaching Critical Thinking
At a training session a couple weeks back, one of my colleagues began complaining about Common Core Learning Standards, the New York version of CCSS. He loudly insisted the problem was that "no educators were involved in the development of CCSS. I did a doubletake, since I've personally spoken with Jason Zimba, a prominent educator and one of the lead authors of the CCSS math standards. The session facilitator told my colleague (I'll refer to him as Jimmy) he was incorrect. Jimmy wouldn't back down. "No, I'm right. It was all done by corporate interests and politicians, and there were no educators involved at any stage of the process.
Besides having met Zimba, I was also on the mailing list when NY State Education Department was considering the standards, and solicited feedback on a number of iterations of drafts. I witnessed as comments were incorporated, and as the CCSS math standards were ultimately adopted with only a few modifications at very early grade levels. So I also told Jimmy he is incorrect. "Prove it to me." he insisted. Since the session was in a computer lab, I went to one of the computers to get him some links to the CCSS documents.
Well, Jimmy refused to look at them. But he did search through his bag, and handed me a worn piece of paper which looked like an unknown generation copy of a copy with headline "Common Core FAQ." As there was no author or source information on the sheet, I asked where it had come from. "I don't know." Jimmy admitted. "But it proves that no educators were involved." I gave the paper back to him, telling him that the unsourced, unattributed copy of a copy was no more than garbage.
End of story? I wish. Today, Jimmy approached me after school. "I hope there are no hard feelings about that disagreement the other day." he offered. I had no hard feelings, and told him so. Jimmy continued, "I didn't like the way you shouted me down."
I had not shouted. I had simply pointed out he was wrong, and pointed out that what he offered as "proof" did not withstand minimal academic standards for a reasoned, cogent argument. So I told him, "It is just that I have personal knowledge of educators who have been involved in the development of Common Core, so I know that you were wrong."
"Well, that's your opinion." he said.
"No," I corrected. "That is not opinion, it is fact. You may not think Common Core is good, and that is opinion. But educators, including some very prominent and well-respected educators, were definitely involved, and that is a fact."
Jimmy walked off, apparently unhappy.
Besides having met Zimba, I was also on the mailing list when NY State Education Department was considering the standards, and solicited feedback on a number of iterations of drafts. I witnessed as comments were incorporated, and as the CCSS math standards were ultimately adopted with only a few modifications at very early grade levels. So I also told Jimmy he is incorrect. "Prove it to me." he insisted. Since the session was in a computer lab, I went to one of the computers to get him some links to the CCSS documents.
Well, Jimmy refused to look at them. But he did search through his bag, and handed me a worn piece of paper which looked like an unknown generation copy of a copy with headline "Common Core FAQ." As there was no author or source information on the sheet, I asked where it had come from. "I don't know." Jimmy admitted. "But it proves that no educators were involved." I gave the paper back to him, telling him that the unsourced, unattributed copy of a copy was no more than garbage.
End of story? I wish. Today, Jimmy approached me after school. "I hope there are no hard feelings about that disagreement the other day." he offered. I had no hard feelings, and told him so. Jimmy continued, "I didn't like the way you shouted me down."
I had not shouted. I had simply pointed out he was wrong, and pointed out that what he offered as "proof" did not withstand minimal academic standards for a reasoned, cogent argument. So I told him, "It is just that I have personal knowledge of educators who have been involved in the development of Common Core, so I know that you were wrong."
"Well, that's your opinion." he said.
"No," I corrected. "That is not opinion, it is fact. You may not think Common Core is good, and that is opinion. But educators, including some very prominent and well-respected educators, were definitely involved, and that is a fact."
Jimmy walked off, apparently unhappy.
Subscribe to:
Comments (Atom)